最近几年,非厄米物理和拓扑物理的交叉——非厄米拓扑物理学的兴起大大改变了传统拓扑物理的体边对应关系。光子晶体又是研究该领域的可靠平台,因此,基于光子晶体研究非厄米拓扑态对新型拓扑器件的设计具有重要意义。
近日,我校理学院“微纳光子和量子调控应用研究所”蒋立勇教授团队在非厄米光子晶体拓扑态领域取得最新进展,相关研究成果发表在光学类top期刊《Optics Express》上,理学院硕士研究生王庆为第一作者,蒋立勇教授为通讯作者,南京理工大学为第一单位。论文题目为“Non-Hermitian kagome photonic crystal with a totally topological spatial mode selection”。
文章链接:https://opg.optica.org/oe/abstract.cfm?uri=oe-31-4-5363
之前基于二维正方声子晶体的典型四极子高阶拓扑绝缘体的研究已经证明通过在PT对称设置中使用平衡增益和损失来修正高阶体边和体角对应关系,即采用不同的PT对称设置时,厄米二维晶格中方形单元胞四角同时激发的常见拓扑角态将被复共轭对角态或伪铰链角态所取代。最近,基于二维方晶格的的进一步工作表明,当考虑更高的增益和损失系数时,复共轭角态可以仅局限于特定的角。也就是说,在这种非厄米系统中可以实现拓扑角态的完全空间模式选择。
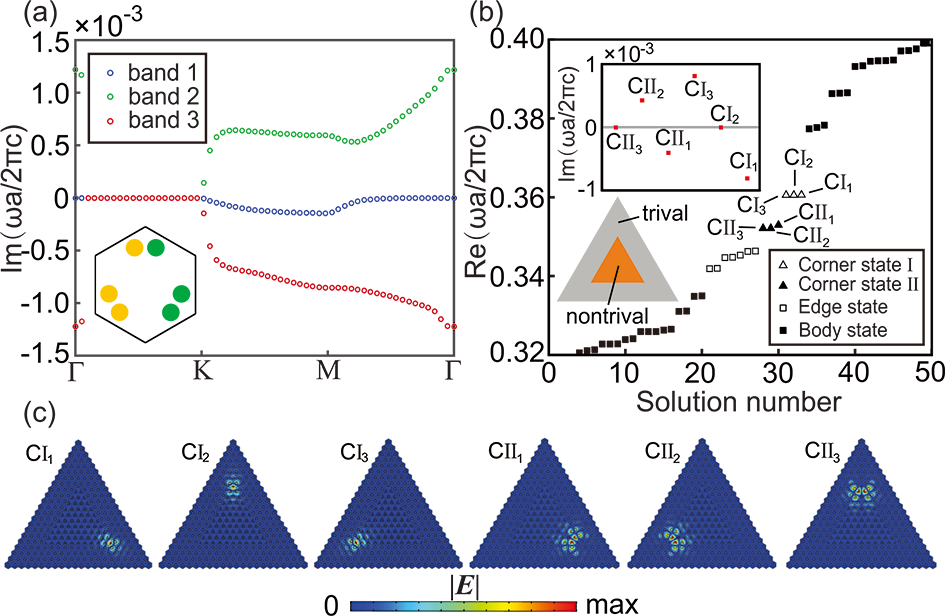
在这项工作中,我们创新性地提出了一个基于含有二聚体单元的Kagome光子晶体的Wannier型高阶拓扑绝缘体模型,并研究了其非厄米拓扑角态。当在适当的PT对称设置下将平衡的增益和损耗引入二聚体单元时,系统将显示不对称的Wannier带,并且可以支持两个厄米角态和两对复共轭或伪复共轭非厄米角态
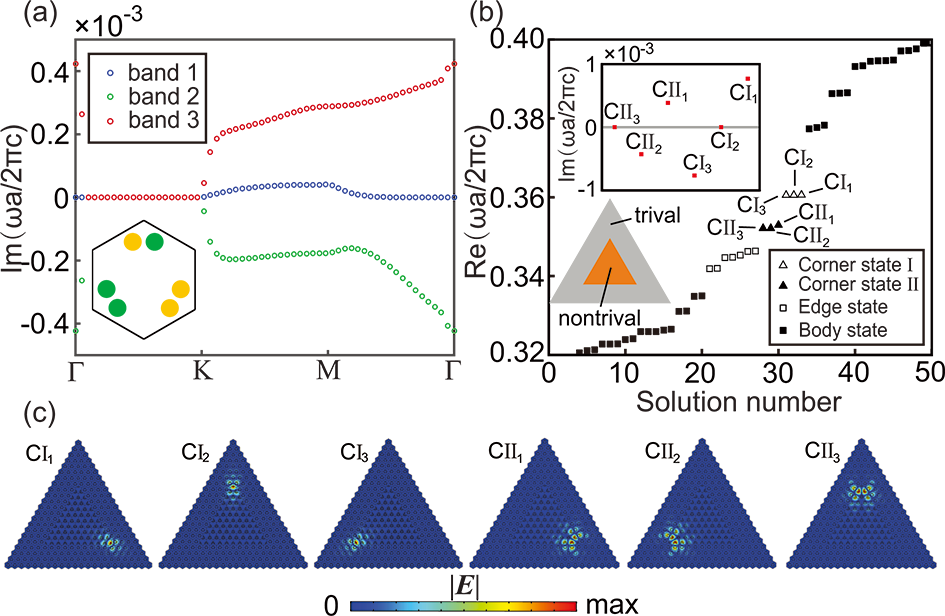
这些拓扑角态被限制于平凡和非平凡Kagome光子晶体构建的三角形超晶胞的三个角与厄米Kagome光子晶体不同的是,三个拓扑角态的特征模式不再简并,分别为一个实角态和一对复共轭的虚角态,而这三个角态的不同特性也正好对应于拓扑空间模式选择效应。
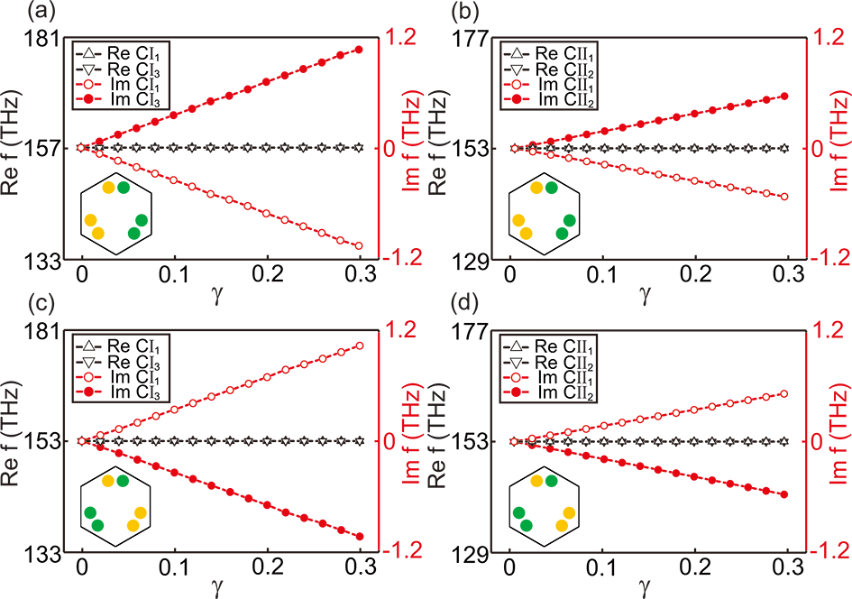
最后,我们计算了复共轭或伪复共轭I型和II型角态的实频和虚频作为增益/损失系数的函数。这些模态的实频率不受增益/损失系数的影响,而虚频率随增益/损失系数的增加呈线性变化。在相同的增益/损失系数下,I型角态比II型角态表现出更明显的分裂虚频。同时,I型角态和II型角态都可以在无阈值的情况下被激发,这意味着该系统可以很容易地实现拓扑角态的全拓扑空间模式选择。这与非厄米二维正方晶格光子晶体有很大不同,后者需要更高的增益/损失系数才能打破PT对称相位,获得完全拓扑的空间模式选择。因此,我们提出的系统将大大降低实验中材料选择的难度。
该工作得到了国家自然科学基金、江苏省“六大人才高峰"高层次人才项目、中央高校基本科研业务费专项资金等项目的资助。




